| Barra di navigazione |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
BALISTICA
La balistica è quel ramo della fisica meccanica che studia il moto dei proiettili. Appare opportuno richiamarne, per completezza di trattazione, la terminologia ed i principi fondamentali di più diretto impiego.
I corpi hanno la proprietà della mobilità e della inerzia.
Dicesi mobilità la facoltà dei corpi di poter occupare successivamente diverse posizioni nello spazio. Un corpo può trovarsi in movimento oppure in stato di quiete o riposo.
Dicesi inerzia la proprietà per la quale un corpo non può da solo modificare il suo stato di quiete o di moto.
Secondo il principio d'inerzia "lo stato di quiete o di movimento di un corpo abbandonato a se stesso non può essere modificato che da una causa esterna agente sul corpo".
Forza è appunto la causa esterna capace di produrre o modificare un moto, cioè di vincere l'inerzia.
Gravità è la forza che fa cadere un corpo solido quando è liberamente abbandonato a se stesso e si manifesta come peso sopra un appoggio che impedisce al corpo di cadere. La forza di gravità agisce su tutte le singole molecole che costituiscono un corpo. Il punto invariabile di un corpo, per cui passa la risultante di tutte le azioni eguali e parallele che la gravità esercita sulle diverse molecole è detto centro di gravità.
Il movimento di un corpo è caratterizzato dalla traiettoria e dalle leggi del moto.
Traiettoria è la linea continua costituita dalle diverse posizioni occupate dal centro di gravità del corpo in tempi successivi (può essere rettilinea, curvilinea, ecc.).
Direzione del moto, in un punto qualunque di una traiettoria curvilinea, è la direzione della tangente alla traiettoria in quel punto.
Legge del moto è la relazione che esiste tra gli spazi percorsi dal corpo ed i tempi impiegati a percorrerli.
Il moto può essere uniforme o vario.
Si dice che un corpo possiede moto uniforme quando in tempi eguali e successivi, comunque piccoli, percorre spazi eguali e nella stessa direzione; vale a dire che gli spazi percorsi dal mobile sono proporzionali ai tempi impiegati a percorrerli.
Dicesi velocità di un moto uniforme lo spazio percorso dal mobile nell'unità di tempo.
La formula del moto uniforme è
S = Vt da cui V =S/t e t = S/V
Nella rappresentazione grafica con assi cartesiani il moto uniforme è rappresentato da una linea retta.
Ogni moto non uniforme è "vario". In esso il rapporto spazio/tempo, cioè la velocità, varia nel periodo considerato.
Poiché la velocità varia da un istante all'altro, non potrà più parlarsi di velocità in genere, ma di velocità istantanea (vale a dire la velocità del mobile in un determinato istante, ovvero velocità che il mobile avrebbe in quel momento se cessasse ogni variazione di rapporto spazio temporale ed il moto diventasse uniforme), e velocità media in un dato intervallo di tempo, (vale a dire la velocità riferita al moto uniforme, con il quale il mobile percorrerebbe lo stesso spazio durante lo stesso tempo).
Il moto vario è accelerato se la sua velocità cresce col tempo, ritardato se decresce.
Se la velocità cresce o decresce proporzionalmente al tempo, il moto dicesi uniformemente accelerato o ritardato.
Accelerazione dicesi la misura costante di cui la velocità cresce o decresce durante ogni unità di tempo. Essa è positiva nel moto uniformemente accelerato, negativa nel moto uniformemente ritardato.
Indicando con "a" l'accelerazione e con "Vo " la velocità iniziale, la velocità finale "V" sarà data da
V = Vo + at per il m.u. accelerato
V = Vo - at per il m.u. ritardato
Se il corpo parte dallo stato di quiete, si ha Vo = 0 e quindi V = at
Graficamente, la curva delle velocità nel moto uniformemente vario è una linea retta. La curva degli spazi è una parabola.
Le formule che descrivono il moto uniforme vario sono riportate nella tavola che segue.
MOTO UNIFORMEMENTE ACCELERATO O RITARDATO
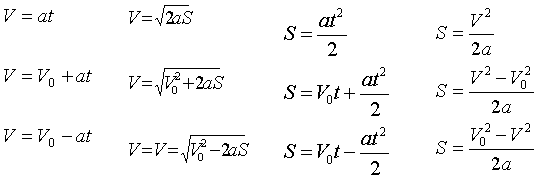
NOTA: Nella prima riga sono riportate le formule per il moto accelerato senza velicità iniziale
Nella seconda riga quelle con velocità iniziale.
Nella terza le formule per il moto uniformemente ritardato.
Se in luogo dell'accelerazione -a- si pone la gravità -g- e in luogo di -S- si pone l'altezza di caduta -H-, le formule risolvono problemi relativi alla caduta dei gravi (m. u. accelerato) o al lancio dei gravi verso l'alto (m. u. ritardato). Le relazioni tra le forze ed i movimenti che esse causano sono studiate dalla dinamica.
Leggi fondamentali della dinamica sono
LEGGE DI INERZIA (Keplero): un corpo in riposo non può mettersi da sé in movimento. Un corpo materiale in movimento non può da sé modificare la misura né la direzione della propria velocità. Da un diverso punto di vista si può dire che un corpo che non subisce influenze esterne non può essere che in quiete o animato da moto rettilineo uniforme.
UGUAGLIANZA DELL'AZIONE E DELLA REAZIONE (NEWTON): tutte le volte che un corpo agisce su di un altro corpo rigido, questi reagisce sul primo con una forza uguale di senso contrario.
MOVIMENTI RELATIVI (Galileo): L'effetto di una forza su di un corpo è indipendentedal movimento anteriormente posseduto dal corpo stesso. Una forza costante che agisce su di un corpo può dar luogo a tre diversi tipi di movimento:
a) agendo su di un corpo libero in quiete, gli imprime un moto rettilineo uniformemente accelerato;
b) agendo su di un corpo animato di velocità iniziale e nella stessa direzione, gli imprime un movimento rettilineo uniformemente accelerato;
c) agendo su di un corpo animato da una velocità iniziale avente diversa direzione, gli imprime un moto parabolico.
La gravità è una forza che può ritenersi costante: perciò un corpo nel vuoto cadrà con moto uniformemente accelerato. I problemi relativi alla caduta dei corpi nel vuoto saranno quindi risolvibili con le formule della tabella 1 sopra riportate in cui l'accelerazione "a" sarà rappresentata dalla gravità "g".
La gravità è misurata dal doppio dello spazio percorso dal corpo durante il primo secondo di caduta ed il suo valore medio sul livello del mare è di m. 9,81 al secondo per secondo.
I valori effettivi variano da 9,781 all'equatore a 9,831 ai poli.
Dalla formula V = Vo - gt si ricava che un corpo lanciato in alto si arresta dopo un tempo t = Vo/g
Inserendo questo valore di t nella formula
H = Vot – (gt²/2)
si ricava che il corpo si arresterà dopo aver percorso lo spazio
H = Vo²/2g
Esempi: Un sasso raggiunge il fondo di un pozzo dopo 5". Quanto è profondo il pozzo, trascurando la resistenza dell'aria?
H= 9,81 x 5²/2 = 122,62 m
Un sasso è lanciato in alto con velocità iniziale di 49 m/sec. Quale altezza avrà raggiunto dopo 3" e quale sarà l'altezza massima raggiunta?
H= 9,81 x 3²/2 = 102,85 m
Il tempo in cui si arresterà
t= 49/9,81 = 5"
L’altezza massima sarà 49²/ (2 x 9,91) = 122,6 m
Quando più forze agiscono simultaneamente su di un corpo, ognuna di esse opera effetti indipendenti dalle altre. Se una delle forze F è il peso P del corpo, l'accelerazione corrispondente sarà quella "g" dovuta alla gravità sicché
F = Pa/g
vale a dire che il valore della forza è misurato dal peso del corpo moltiplicato per il rapporto fra accelerazione "a" dovuta alla forza e quella "g" dovuta alla gravità.
Massa è il rapporto fra il peso del corpo e l'accelerazione di gravità
M =P/G da cui P= Mg
o, in generale,
F = Ma
Il prodotto Ma rappresenta la misura dinamica di una forza: l'intensità di una forza è uguale al prodotto della massa del corpo a cui è applicata per l'accelerazione del movimento che essa produce.
Esempi: Sopra un corpo che pesa 300 Kg. agisce una forza costante che produce l'accelerazione di 3 m/sec². Determinare F
F = 300 x 3 / 9,81 = 91,74 kg
-Che accelerazione produrrà su di un corpo pesante 500 kg. una forza costante di 50 kg?
a = 50 x 9,81 / 500 = 0,981 m/sec
-Che forza ha agito su di un corpo pesante kg.2000 per farlo passare in 15" dalla velocità di 10 m/sec alla velocità di 115 m/sec. ?
V= Vo + at; 115 = 10 + 15a; a = 7 m/sec
F = 200 x 7 / 9,81 = 1427 kg
L'unità di massa è quella di un corpo al quale la forza di un kg. imprime l'accelerazione di 1 m/sec².
L'unità di forza è quella forza che agendo sull'unità di massa le imprime l'accelerazione di 1 m/sec² .
La "quantità di moto" di un corpo in movimento è il prodotto MV della sua massa per la velocità che esso possiede nell'istante considerato.
Da ciò il principio importantissimo che le velocità impresse da una stessa forza a corpi di massa diversa sono inversamente proporzionali alle masse dei corpi ed ancora, che quando una determinata forza agisce per lo stesso tempo su corpi di massa diversa, la quantità di moto è la stessa; in pratica quello che si guadagna in massa posta in movimento, si perde in velocità e viceversa.
Una forza quindi imprime a due corpi di peso diverso velocità inversamente proporzionali ai rispettivi pesi:
V : V’ = P’ : P
Una forza imprime a due corpi di peso diverso accelerazioni inversamente proporzionali alle rispettive masse.
M : M’ = a’ : a
L'impulso è il prodotto di una forza per il tempo durante il quale essa agisce. L'impulso di una forza costante agente su di un corpo che parte dalla quiete è eguale alla quantità di moto
Ft = MV
Non esistono forze istantanee.
Forza di inerzia è quella forza contraria alla forza F e capace di equilibrarla.
Il lavoro di una forza costante applicata ad un corpo è dato dal prodotto dell'intensità della forza agente nel senso del moto per lo spazio percorso dal corpo
L = FS
Unitàdilavoro è il chilogrammetro(kgm )che corrisponde al sollevamento del peso di un kg. all'altezza di un metro. Questo valore è indipendente dalla durata, cioè dal tempo impiegato a compiere il lavoro.
Nel nuovo sistema di unità di misura si usa il Joule; 1 kgm = 9,81 J
Forza viva: se un corpo è dotato di moto di traslazione, dicesi forza viva il prodotto della sua massa per il quadrato della sua velocità M.V².
Affinché un corpo di massa M dalla quiete venga messo in moto con una data velocità V, occorrerà spendere, un lavoro eguale alla metà della forza viva
L = MV²/2
detto anche energia cinetica.
Se il corpo già possedeva una velocità iniziale V si avrà
L = M(V² - Vo²)/2
Inversamente, un corpo in movimento che si ferma è capace di produrre un lavoro. eguale a quello speso per metterlo in movimento e per fargli acquistare la velocità prima posseduta.
URTO DEI CORPI
Teorema di Carnot: nell'urto tra corpi anelastici o molli si verifica sempre una cessione di forza viva e perciò di lavoro; nello urto tra corpi perfettamente elastici non vi è perdita di forza viva e non si perde quindi lavoro. Nell'urto tra due corpi M e M' molli che si muovono nella stessa direzione con velocità V e V', la velocità comune Vo dopo l'impatto sarà
Vo = (MC+ M’V’)/(M+M’)
Se i corpi si muovono in senso contrario si avrà
Vo = (MV – MV’)/(M+M’)
e quindi in generale
Vo = (MV± M’V’)/(M+M’) = (PV± P’V’)/(P+P’)
Se uno dei due corpi è fermo e quindi V' = 0 si avrà
Vo = MV/(M+M’)
Nell'urto diretto fra corpi elastici, in pratica, vi è uno scambio di velocità. La perdita di velocità subita dal corpo urtante è doppia di quella che avrebbe subito se il corpo fosse stato anelastico; la velocità acquistata dal corpo urtato è doppia di quella che avrebbe acquistato se fosse stato anelastico. Dati quindi i due corpi elastíci A e B che si muovono stessa direzione con velocità V e V' , le velocità Va e Vb dopo l'urto, e con Vo la velocità che avrebbero acquistato se anelastici, sarà
Va = 2V0 – V e Vb = 2V0 – V’
Se le masse dei due corpi fossero eguali, si avrebbe un esatto scambio di velocità; se il corpo urtato fosse fermo e di egual massa di quello che lo investe, si arresterebbe, mentre quello urtato si muoverebbe con la velocità del primo.
Conversione di misure anglosassoni
moltiplicando per si ottiene
cm 0,3937 pollici
pollici 2,540 cm
metri 3,2808 piedi
piedi 0,3048 m
metri 1,0936 yarde
yarde 0,914 m
metri 39,37 pollici
km 0,6214 miglia
miglio 1,6093 km
miglio mar. 1,852 km
m/s 3,2808 ft/s
ft/s 0,3048 m/s
m/s 3,60 km/h
km/h 0,2778 m/s
ft/s 0,6818 m.p.h.(miles per hour)
m.p.h. 0,447 m/s
cm² 0,1550 sq.in.
sq.in. 6,4516 cm²
m² 10,764 sq. ft.
s q. ft. 0,0929 m²
cm cub 0,061024 cu.in.
cu.in. 16,387 cm cub
dcm cub 0,0353 cu.ft.
cu.ft. 28,317 dcm cub
metro cub 35,315 cu.ft.
1 (litro) 1,76 pinte
grammo 15,432 grs (grani)
gr.(grano) 0,0648 grammo
grammo 0,564 drs (dracme)
drs 1,772 grammo
grammo 0,0353 oz (once)
oz 28,349 grammo
kg 2,2046 lbs (libbre)
lb 0,45359 kg
t(tonnellate) 0,9842 ton
ton. 1,016 t
kgm. 7,233 ft.lb.
ftlb. 0,1383 kgm
at (kg/cm²) 14,227 psi(pounds/square inch)
psi 0,0703 at
BALISTICA ESTERNA
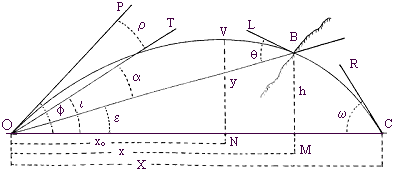
Nomenclatura della traiettoria
Traiettoria è la linea curva percorsa nello spazio dal centro di gravità del proiettile durante il suo movimento.
O Origine della traiettoria; è il centro della bocca dell'arma (volata) al momento della sparo.
B Punto di arrivo e cioè il bersaglio mirato; è il punto in cui la linea di sito interseca la traiettoria.
C Punto di caduta; corrisponde all'intersezione del ramo discendente della traiettoria con la linea di orizzonte dell'arma. Può coincidere con il punto B se questo si trova sulla linea di orizzonte.
V Vertice della traiettoria, cioè il punto più alto che la divide nel ramo ascendente (OV) e nel ramo discendente (VC).
OP Linea di proiezione; è il prolungamento dell'asse della canna al momento in cui il proiettile abbandona l'arma; in termini geometrici è la tangente all'origine della traiettoria.
OT Linea di tiro. È il prolungamento dell'asse della canna puntata, prima dello sparo; passerà nella posizione P per effetto del rilevamento.
OB Linea di sito di un punto B della traiettoria; è la retta che congiunge l'origine della traiettoria col punto stesso; è cioè la linea retta che congiunge la volata con il bersaglio.
x Ascissa di un punto B (ad es. OM), è la distanza del punto B dall'origine misurata sull'asse orizzontale.
xo Ascissa al vertice (ON).
X Gittata OC, è la distanza tra l'origine e il punto di caduta.
Y Altezza della traiettoria o ordinata massima o ordinata al vertice; è il punto della traiettoria più alto sulla linea dell'orizzonte.
h Ordinata di un punto B (es. BM), è l'altezza del punto B rispetto all'orizzonte.
BOC Angolo di sito e .
POB Angolo di partenza g .
POC Angolo di proiezione f compreso fra la linea di proiezione e l'orizzonte .
POT Angolo di rilevamento r ; è l'angolo formato dalla linea di proiezione con la linea di tiro.
TOB Angolo di elevazione a ; è l'angolo formato dalla linea di tiro con la linea di sito e corrisponde al cosiddetto alzo.
TOC Angolo di tiro i che la linea di tiro forma con l'orizzonte.
OCR Angolo di caduta w è l'angolo acuto formato dalla tangente alla traiettoria nel punto di caduta con la linea d'orizzonte.
OBL Angolo di arrivo q ; è l'angolo formato dalla tangente alla traiettoria con la linea di sito nel punto di arrivo B; non confonderlo con l'angolo di impatto che è l'angolo formato dalla tangente alla traiettoria con il terreno nel punto B e dipende perciò dall'andamento del terreno.
La balistica è quel ramo della fisica che studia il moto dei proiettili che avviene all'interno della canna dell'arma (balistica interna), nello spazio esterno (balistica esterna) e, infine, entro il bersaglio colpito (balistica terminale).
Nello spazio esterno il proiettile percorre una traiettoria che è il risultato di tre distinte forze (qui trascurando dati che interessano solo per missili o proiettili a lunghissima gittata): l'impulso iniziale che gli imprime un moto uniforme e rettilineo, la resistenza dell'aria che si oppone ad esso in senso contrario, la forza di gravità che tende a far cadere il proiettile verso il suolo con moto uniformemente accelerato.
La resistenza dell'aria assume un ruolo rilevante per proiettili veloci e quindi, per proiettili molto lenti (artiglierie antiche, frecce, sassi) può essere pressoché trascurata (per un mortaio ottocentesco la differenza rispetto alla traiettoria nel vuoto era soltanto del 10%).
Il calcolo del moto di un proiettile nel vuoto è alquanto semplice.
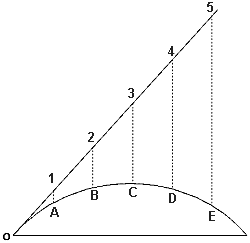
ricaviamo che dopo un secondo (t) il proiettile sarà caduto dello spazio s fino al punto A, dopo due secondi fino al punto B, dopo tre secondi fino al punto C, e così via. Collegando tutti i punti A, B, C, ... si ottiene la traiettoria percorsa dal proiettile. Essa è rappresentata da una parabola simmetrica in cui l'angolo di partenza è eguale all'angolo di caduta, la velocità iniziale è eguale alla velocità finale e il vertice la divide in due rami simmetrici. Essa può essere calcolata conoscendo solo i parametri V (velocità iniziale) e (angolo di partenza).
La gittata X si ottiene dalla formula
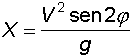
da cui si deduce che la gittata massima si ottiene con un angolo di partenza di 45° quando il valore del seno dell'angolo è eguale ad uno; il che significa, ad esempio, che, trascurando la resistenza dell'aria, una freccia lanciata alla velocità di 100 m/s arriva al massimo alla distanza di 1019 metri.
Il tempo di volo del proiettile fino ad una data distanza è dato da
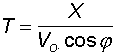
Quando il moto del proiettile invece che nel vuoto avviene nell'aria, assume importanza fondamentale la forza ritardatrice dovuta alla resistenza del mezzo. Un proiettile cal. 9 Para con V0 = 330 m/s, che nel vuoto avrebbe una gittata massima di 11.100 metri, nell'aria ha una gittata massima di circa 1500 metri; un proiettile di moschetto è assoggettato ad una forza ritardatrice che riduce la sua velocità finale ad 1/6 di quella iniziale. La traiettoria percorsa non è quindi simmetrica, ma ad un ramo ascendente più lungo, segue un ramo discendente più curvo e corto così che l'angolo di caduta è maggiore dell'angolo di partenza.
In linea generale la traiettoria è tanto più curva quanto più lento è il proiettile per il fatto che la forza di gravità agisce più a lungo. Il peso del proiettile, a parità di velocità, non incide sulla maggiore o minore curvatura della traiettoria ed in teoria, a parità di forma e di velocità iniziale, il maggior peso rende più tesa la traiettoria, sia pure in misura trascurabile alle distanze venatorie (infatti se il proiettile pesa di più, a parità di calibro aumenta la sua lunghezza e la densità sezionale e migliora quindi il suo comportamento balistico). In pratica però, specie nelle armi leggere, il proiettile più pesante viene sparato a velocità inferiori rispetto ad un proiettile leggero, con la conseguenza che la sua traiettoria sarà meno tesa.
Il calcolo della resistenza dell'aria e della relativa ritardazione, è semplice per velocità inferiori ai 200 m/s per cui si può assumere che la resistenza vari con tasso inferiore al quadrato della velocità, ma diventa difficile a velocità superiori in cui essa varia con un tasso assai maggiore, con un'impennata per velocità prossime al muro del suono, ed è influenzata da numerosi fattori, quali la densità dell'aria alle diverse altezze raggiunte (e con il variare della densità varia la velocità del suono e quindi la ritardazione), i moti di oscillazione e di precessione del proiettile durante il volo, ecc. Ovviamente poi la resistenza varia a seconda della forma più o meno aerodinamica del proiettile e risultati precisi si possono ottenere solo su basi sperimentali, redigendo per ogni proiettile apposite tavole di tiro, cosa che fa ogni esercito per le sue artiglierie.
Per calcoli di una certa approssimazione, si sono però studiate delle leggi generali di resistenza dell'aria, più che sufficienti per scopi pratici: dopo aver tracciato sperimentalmente le curve della resistenza dell'aria riferite a diversi tipi di proiettile, si è ricavata una curva intermedia teorica o riferita ad un proiettile tipo; da questa, introducendo un coefficiente (coefficiente balistico, ricavato dal suo calibro e dal suo peso, integrato dal coefficiente di forma "i", ricavato dalla forma del proiettile), che indicano il rapporto tra proiettile tipo e proiettile in esame, si risale ai valori reali.
La formula per il coeff. balistico è data da
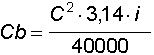
in cui il calibro C è espresso in millimetri. Il valore di i è il dato più difficile da calcolare anche perché varia in relazione alla velocità; in via di prima approssimazione si può ritenere che esso vari da 0,44 per proiettili appuntiti, tipo quelli per moschetto militare, a 1 - 1,2 per proiettili da pistola o rivoltella, fino a 3 - 4 per proiettili cilindrici (wad cutter).
In tempi più recenti in luogo del concetto di coefficiente balistico si è introdotto quello di coefficiente aerodinamico Cx che per i proiettili varia da 0,1 a 0,5. Anch'esso non è costante, ma varia in relazione alla velocità espressa in Mach.
Il calcolo di una traiettoria di un proiettile moderno è comunque estremamente complicato e richiede l'impiego di matematiche superiori. Si può ovviare con l'impiego di metodi grafici o di tavole di ritardazione già compilate, ma si tratta comunque di attività laboriose. Attualmente sono in commercio numerosi programmi di balistica per computer, limitati però a traiettorie di pratico impiego, di poche centinaia di metri e tese, in cui l'angolo di proiezione non supera i 5°.
La gittata massima
Non è possibile indicare una semplice formula matematica che consenta di calcolare con buona approssimazione la gittata massima di un proiettile, cioè la massima distanza a cui il proiettile può arrivare nella migliore delle ipotesi.
In via molto approssimata può usarsi la mia formula
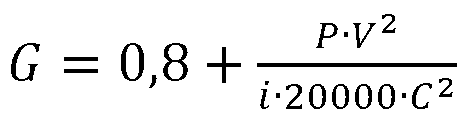
in cui P è il peso in grammi, V la velocità in m/s, C il calibro in millimetri ed i il fattore di forma. Essa è valida principalmente per proiettili oltre i 10 mm.
Un'altra formula approssimativa richiede la conoscenza della velocità iniziale e della velocità residua ad una data distanza y.
La gittata massima sarà data da
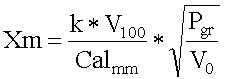
in cui k è un coefficiente pari a 300 per proiettili da pistola e 400 per proiettili per fucile.
Nel vuoto, come detto, la gittata massima si ha con un angolo di proiezione di 45°. Nell'aria l'angolo è inferiore (salvo il caso di proiettili di grosso calibro con velocità iniziale superiore a 1400 m/s che viaggiano per un tratto negli strati alti dell'atmosfera) e, per proiettili di armi portatili l'angolo ottimale è compreso tra i 30° ed i 35°, tenendo però presente che la gittata non cresce di molto oltre un certo angolo; così, ad es., un proiettile militare cal. 7,62x54 che con un angolo di 35° raggiunge la gittata massima di 3650 m., con un angolo di 19° raggiunge una gittata di circa 3500 m, inferiore di soli 150 m.
Per un orientamento generale si riportano le gittate massime dei più comuni proiettili per armi leggere.
| Calibro |
Velocità m/s |
Gittata in m. |
| 4,5 mm aria compressa |
120/165 |
100/150 |
| 4,5 mm aria compressa |
200/250 |
200/300 |
| 6/9 mm Flobert |
225 |
700 |
| .22 corto |
260 |
1000 |
| .22 Long Rifle |
350 |
1370 |
| .22 Long Rifle HS |
370 |
1500 |
| .22 Winch. Magnum |
610 |
1800 |
| 243 Winch. |
1070 |
3200 |
| 6,35 mm |
220 |
800 |
| 7,65 mm |
285 |
1300 |
| 9 mm corto |
285 |
1300 |
| 9 mm Para |
350 |
1700 |
| .45 ACP |
300 |
1620 |
| 30 M1Carb. |
600 |
2000 |
| 7x70 mm |
830 |
3500 |
| 8x57 mm JS |
830 |
3500 |
| 6,5x57 mm |
1020 |
4000 |
| 7x57 mm |
850 |
4500 |
| 6,5x68 mm |
1150 |
5000 |
Siccome la mia formula non è il massimo per precisione, riporto un utile nomogramma che consente di calcolare i valori per la gittata massima. Non va bene per piccoli proiettili, perché il valore di ingresso nella tavola è troppo piccolo.
Nomogramma per la gittata massima, tempo di volo e angolo di proiezione
Il seguente nomogramma, tratto dal manuale della Rheinmetall, consente di calcolare graficamente e con buona approssimazione la gittata massima in relazione a calibro e peso del proiettile ed alla velocità iniziale.
Esso è basato su di un proiettile teorico (legge di resistenza della Rheinmetall) con Cx= 2 alle basse velocità, e Cx = 4 alle velocità supersoniche.
In rapporto alle leggi di resistenza su cui si basano le tavole usuali (Siacci, Saengewald) si ha i=1 fino alla velocità di 320 m/s; da 360 m/s in poi si può assumere i=1,5
In relazione alla gittata massima individuata si può leggere poi e l'angolo di proiezione che consente di ottenerla e il relativo tempo di volo.
Facendo un esempio pratico, si procederà così: Calibro 26 mm (raggio 13 mm)
Peso 440 gr.
Vo 600 ms
Occorre trovare il valore da 0 a 40 con cui entrare nella tavola ed esso sarà dato dal fattore di forma i diviso per la densità sezionale Q (kg/mq); se il proiettile ha forma standard i=1 il valore ricercato è dato dal valore reciproco di Q. La superficie della sezione sarà data da 3,14 x 13² = 530 mmq e quindi il valore ricercato, moltiplicato per 10 al fine di eliminare inutili virgole, sarà dato da
10* i / (440/530)= 12
Se ora dal valore 12 eleviamo una perpendicolare fino ad incontrare la linea continua per il valore di 600 ms, troviamo che l'incrocio avviene ad un valore di gittata massima pari a 8 Km. Lo stesso punto di incrocio ci dice che l'angolo di proiezione che consente la gittata massima è di circa 41° e che il tempo di volo è di circa 45 secondi.
Il nomogramma va stampato con buona definizione ed in formato A4 e perciò lo unisco zippato.
Nomograma zippato di 156 Kb
Il tiro verticale
Un proiettile sparato verticalmente verso l'alto raggiunge un'altezza pari a circa il 70% della gittata massima. Nel ricadere verso il basso il proiettile aumenta progressivamente la sua velocità, come qualsiasi corpo in caduta libera, finché la ritardazione dovuta alla resistenza dell'aria non eguaglia la forza di gravità; da quel momento la velocità del proiettile rimane costante (velocità limite). Se il proiettile è stato sparato proprio verticalmente, e quindi non compie alcuna traiettoria, ricadrà con il fondo piatto verso il suolo e offrirà una grande resistenza all'aria così che la sua velocità finale sarà di circa 30-50 m/s, non idonea a provocare lesioni ad una persona. Se è stato sparato con un piccolo angolo rispetto alla verticale, si capovolge e ricade con la punta in avanti; un proiettile di pistola può raggiungere i 100 m/s e uno di moschetto i 180 m/s, del tutto idonei a provocare gravi lesioni (si consideri che quest'ultimo può ancora penetrare per 30-40 cm nel corpo umano).
Il proiettile ricade in genere nel raggio di una decina di metri dal tiratore, ma può essere spostato dal vento anche di 200 metri. Il tempo che un proiettile di moschetto impiega a ricadere è di circa 30 secondi se con la punta in avanti e di oltre il doppio se è capovolto, il che può dar luogo a ferite apparentemente inspiegabili.
L'influenza del vento
L'influenza del vento che spira a favore o contro il proiettile può essere trascurato per le normali distanze d'impiego delle armi leggere. Ha invece un'influenza significativa quando soffia trasversalmente alla traiettoria. Il calcolo può essere solo molto approssimativo poiché il vento non è costante, ma soffia a raffiche e non ha velocità costante poiché essa varia in relazione ad ostacoli ed alla distanza dal suolo. Supposto comunque che si possa ipotizzare una certa velocità e che il vento soffi perpendicolarmente alla traiettoria, trova applicazione la formula di Didion la quale ci dice che lo spostamento D, in metri, del proiettile dal punto mirato, ad una data distanza X, è dato dalla velocità del vento W moltiplicata per la differenza tra tempo di volo nell'aria T e tempo di volo nel vuoto per il valore di X considerato, e cioè
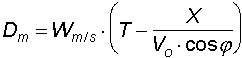
A titolo di esempio si consideri che un vento di 10 m/s (vento sensibile che alza polvere e piega alberelli), sposta un proiettile di fucile militare, su di un bersaglio posto a 300 metri, di circa 50 cm.
Se il vento non è perpendicolare ma forma un certo angolo "a " con la traiettoria, il risultato D dovrà essere moltiplicato per il valore di cos2a .
Densità dell'aria
La densità dell'aria determina la resistenza al moto del proiettile e, come si è visto, entra in tutte le formule concernenti la resistenza dell'aria Essa varia in relazione alla temperatura ed alla pressione atmosferica e, in misura minore in relazione all'umidità.
Con formula molto approssimata, la densità dell'aria, che viene essere assunta pari a 1,225 kg/mc nell'atmosfera standard al livello del mare ed alla temperatura di 15 gradi, può essere calcolata con la seguente formula, nota la temperatura e la pressione atmosferica in millimetri di mercurio,
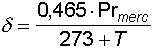
Ricordo che la pressione in mm di mercurio si ottiene moltiplicando la pressione in millibar per 0,75 e che la temperatura, in linea di massima, diminuisce di 0,65 gradi quando si sale di 100 metri.
Quando non si conosce la pressione atmosferica ma solo l'altitudine H del luogo ove si sviluppa la traiettoria del proiettile, la formula di cui sopra diventa
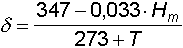
Per gli usi normali di un'arma nelle nostre regioni, la densità dell'aria può però essere trascurata dallo sparatore; in genere la diminuzione di densità dovuta al crescere dell'altitudine, viene compensata dalla diminuzione di temperatura e, comunque, il fatto di sparare in un'atmosfera meno densa, come avviene in alta montagna, comporta un miglioramento della traiettoria che sarà più tesa.
La derivazione del proiettile
Una canna rigata ha al suo interno le cosiddette righe che, come la filettatura di di una vite, si sviluppano con un certo passo (tratto di canna in cui il proiettile compie una intera rotazione su se stesso)e con un certo angolo di rigatura (inclinazione della rigatura rispetto all'asse longitudinale della canna); il rapporto che lega l'angolo di rigatura con il passo è dato dalla formula
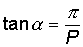
in cui P indica il passo espresso in calibri.
La velocità di rotazione dei proiettile è data dalla formula
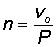
in cui v è la velocità alla bocca.
La rotazione del proiettile nell'aria provoca l'insorgere di forze, dovute all'effetto Magnus e all'effetto giroscopico che spostano il proiettile lateralmente. Fino ad angoli di elevazione non superiori a 60-70 gradi gradi lo spostamento è vero destra se la rigatura è destrorsa, verso sinistra se la rigatura è sinistrorsa. Al di sopra dei 70 gradi la direzione dello spostamento diviene oscillante e dopo gli 80 gradi si inverte (a sinistra per rigatura destrorsa.)
Per gittate brevi questa derivazione del proiettile viene corretta mediante la taratura dei congegni di mira. In armi in cui non vi sono congegni di mira, oppure per distanze che superano quella per cui i congegni sono tarati, occorre tener conto della derivazione, per nulla trascurabile e che, con buona approssimazione è data dalla formula
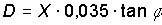
in cui X è la gittata in metri e l'angolo è quello di proiezione.Il risultato D è espresso in metri.
Un'altra formula, ancora più approssimata ci dice che la derivazione, in metri, è pari a 0,11 moltiplicato per il tempo di volo al quadrato (il valore 0,11 è un valore medio che andrebbe calcolato per ogni proiettile).
Raccolta di formule approssimate
Qui di seguito riporto alcune formule molto approssimative che consentono di ottenere valori orientativi partendo da altri valori noti.
1) Ordinata per una distanza x non troppo grande
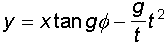
2) Angolo di proiezione nota la gittata massima
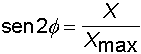
3) Angolo di proiezione noto il tempo di volo
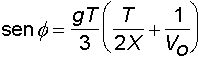
4) Ordinata massima
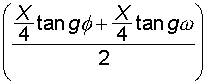
5) Ordinata massima noto il tempo di volo (formula di Haupt)
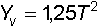
6) Ordinata massima noti gittata e angoli di partenza e caduta
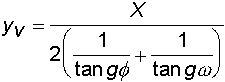
7) Ascissa del vertice nota la gittata
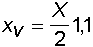
8) Ascissa del vertice nota la gittata e la velocità iniziale
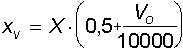
9) Ascissa del vertice noti la gittata, l'ordinata e l'angolo di partenza
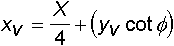
10) Velocità del proiettile al vertice
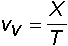
11)Angolo di caduta noti tempo di volo, gittata e velocità di caduta
12) Angolo di caduta noti gittata, ordinata e angolo di partenza
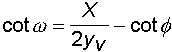
13) Velocità di caduta
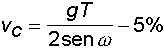
Tavola di raffronto tra i valori calcolati con le formule approssimate e i valori effettivi
| Formula |
Cal. 8x57
calcolato esatto
|
Cal 9 Para
calcolato esatto
|
Cal.7,5 cm =10°
calcolato esatto
|
Cal.7,5 cm =40°
calcolato esatto
|
| 1 y |
|
|
79,3 79 |
|
| 3 f |
2°47' 3°7'30" |
9°48' 11° |
10°2' 10° |
45°8' 40° |
| 4 yv |
38 m 41 |
94 85 |
99,3 99 |
1251 1251 |
| 5 " |
37,95 41 |
82 85 |
101 99 |
1237 1251 |
| 6 " |
36 41 |
82 85 |
99 99 |
1255 1251 |
| 7 xv |
1100 m 1168 |
660 740 |
1188 1102 |
2980 2833 |
| 8 " |
1151 1168 |
639 740 |
1136 1102 |
2850 2833 |
| 9 " |
1250 1168 |
737 740 |
1101 1102 |
2854 2833 |
| 10 Vv |
|
|
240 239,6 |
170 170 |
| 11 w |
6°38' 6°6' |
24°36' 25° |
10°54' 10°50' |
54° 45°25' |
| 12 " |
9°20' 6°6' |
27°34' 25° |
10°48' 10°50' |
45°45' 45° 25' |
| 13 Vc |
253 m/s 245 |
89 81 |
241 230 |
209 208 |
| 14 X-x |
|
|
345 349 |
1298 1466 |
| 15 " |
|
|
340 349 |
1298 1466 |
| 16 h |
|
|
66 55 |
1084 1029 |
| 17 t |
|
|
7",6 7",47 |
23" 22",35 |
| 18 T |
5",7 5",51 |
8",6 8",1 |
8",8 9" |
23" 31",92 |
| 19 T |
5",22 5",51 |
7",6 8",1 |
9",75 9" |
33",7 31",92 |
| 20 y |
41,37m 41 |
101 85 |
99 99 |
1235 1231 |
BALISTICA INTERNA
BALISTICA INTERNA
Volata di una canna con rigatura ed i "pieni" e "vuoti".
La balistica interna studia i fenomeni che accadono dal momento della percussione dell'innesco della cartuccia fino al momento in cui il proiettile esce dalla bocca dell'arma, divenendo oggetto di studio della balistica esterna.
A seguito della violenta percussione del percussore sulla capsula dell'innesco, la composizione innescante viene schiacciata contro l'incudinetta della capsula (nel caso della percussione anulare l'innesco viene schiacciato contro il metallo dell'orlo del fondello); la composizione detona producendo un intenso dardo di fiamma che, attraverso i fori dell'innesco, raggiunge la carica di polvere, dando inizio alla sua deflagrazione.
Questa sarà più o meno veloce in relazione alla forza dell'innesco, al tipo, conformazione e quantità della polvere, alla densità di caricamento (rapporto tra volume della polvere e spazio nella cartuccia), alla compressione esercitata sulla polvere, alla forza con cui il proiettile è trattenuto dal bossolo, ecc.. La polvere deve poter bruciare completamente prima che il proiettile esca dalla canna, sia perché così tutta l'energia viene sfruttata, sia per evitare che i residui si infiammino fuori della bocca dell'arma (vampa di bocca).
La polvere brucia sempre perpendicolarmente alla sua attuale superficie e la quantità di gas prodotti dipende in ogni istante dalla pressione sviluppatasi e dalla forma geometrica dei granelli di polvere. Se la superficie del granello diminuisce durante la combustione (granelli tondi o a lamelle), si ha una polvere degressiva (offensiva), se aumenta (grani o tubetti con più fori) si ha una polvere progressiva; se rimane costante (tubetto con un foro) si ha una polvere neutrale. La velocità di deflagrazione può venire influenzata da trattamenti della superficie del grano.
Le polveri offensive sono più indicate per armi a canna corta in cui non ha senso una pressione che si esplica dopo che il proiettile ha abbandonato l'arma; le polveri progressive sono preferite nelle armi a canna lunga e in tutti quei casi in cui si preferisce non sottoporre ad eccessive sollecitazioni le pareti dell'arma.?
La deflagrazione della polvere sviluppa una grande quantità di gas (circa un litro per ogni grammo di polvere) che si dilatano per effetto del calore (oltre 2000 gradi); un litro di gas, racchiuso in uno spazio minimo e sottoposto a tale temperatura produce un aumento di pressione che in un fucile a palla giunge a superare i 3000 kg/cm2 (circa 500 atmosfere in un fucile a canna liscia). La pressione così sviluppatasi si esercita in tutte le direzioni: contro le pareti del bossolo che viene pressato contro la parete della camera di scoppio (così assicurando che non sfuggano gas all'indietro), contro il fondello che viene premuto contro l'otturatore, contro il fondo del proiettile che viene spinto in avanti; essa continua a crescere fino al momento in cui il proiettile si svincola dal bossolo e inizia il suo percorso. aumenta quindi lo spazio a disposizione per i gas, ma fino a che la produzione di gas è maggiore dello spazio a disposizione, continua ad aumentare la pressione, il che aumenta la produzione di gas. Raggiunto l'equilibrio tra i due valori, la pressione inizia a calare. La combustione deve essere regolata in modo da non superare certi valori di pressione massima e di pressione alla bocca ed in modo che la combustione si concluda all'interno della canna. Il picco di pressione massima si verifica molto presto, in genere da alcuni millimetri a pochi centimetri di percorso del proiettile e la pressione alla bocca deve essere cinque o sei volte minore.
Durante il percorso nella canna il proiettile viene costantemente accelerato nel suo moto così che esce dalla bocca con il massimo della velocità. La pressione invece si riduce a poche centinaia di atmosfere. In genere in un'arma leggera l'aumento della lunghezza della canna non comporta alcun aumento della velocità del proiettile oltre i 60-70 cm. di lunghezza. Nelle armi a canna liscia a pallini, accurati esperimenti hanno dimostrato che, a parità di strozzatura, oltre i 60 cm di lunghezza si ha un aumento di velocità pari a circa 1 m/s per ogni centimetro in più e quindi, nella pratica, un aumento trascurabile.
Un parametro importante nei calcoli di balistica interna è data dal "rapporto di espansione" (inglese: expansion rate) che dà il rapporto tra pressione massima, pressione alla bocca, volume interno della canna e volume interno del bossolo:
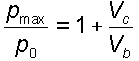
Altro importante parametro è dato dal rapporto tra pressione media e pressione massima.
Il valore della pressione media è dato dalla formula
in cui
m = peso del proiettile in g (dovrei dire massa, ma peso è più chiaro!)
mc = peso della polvere in g
Vo = velocità alla bocca in m/s
S = sezione della canna in mm quadrati
L = spazio libero percorso dal proiettile
Il valore della pressione massima deve essere misurato sperimentalmente oppure ricavato dalle tabelle dele munizioni o di ricarica delle varie polveri.
Calcoli di balistica interna
Il balistico tedesco Heydenreich, sulla base di esperimenti compiuti all'inizio del secolo, ha elaborato una serie di formule empiriche che consentono di eseguire i principali calcoli di balistica interna con accettabile approssimazione.
Sia
Pm = pressione media
Pmax = Pressione massima
Xpmax = Spazio percorso dal proiettile fino al raggiungimento della pressione massima
Vpmax = Velocità del proiettile al raggiungimento della pressione massima
Tpmax = Tempo impiegato a raggiungere la pressione massima
Po = Pressione alla bocca
Xo = Percorso del proiettile fino alla bocca
Vo = Velocità del proiettile alla bocca
To = Tempo impiegato dal proiettile per raggiungere la bocca
Px = Pressione dopo che il proiettile ha percorso lo spazio x
Vx = Velocità dopo che il proiettile ha percorso lo spazio x
Tx = Tempo impiegato a percorrere lo spazio x
I valori ricercati potranno essere calcolati agevolmente mediante l'uso della prima tabella di valori, sulla base della conoscenza di
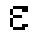 con le seguenti formule:
Una seconda tabella consente invece di calcolare pressione, velocità e tempi in relazione allo spazio percorso, conoscendo il valore
del rapporto tra spazio percorso e Xpmax.
Le formule da applicare sono:
Px = Pmax · G
Vx = Vpmax · H
Tx = Tp · J
Quindi, se sono noti la pressione massima e la velocità alla bocca di una cartuccia, è possibile calcolare i valori lungo tutto il percorso del proiettile entro la canna.
Vediamo un esempio pratico di calcolo (da Beat P. Kneubuehl, Geschosse, 1994)
Sia un proiettile cal. 38 del peso di g. 10,2. Il peso della polvere sia 0,26 g., lo spazio libero percorso dal proiettile 123 mm, (alla lunghezza della canna va aggiunta la lunghezza del proiettile) la velocità alla bocca 265 m/s, la pressione massima 1600 bar, la sezione della canna 62,77 mm quadrati. Si avrà
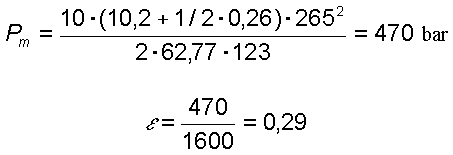
E quindi:
Xpmax = 123·0,0383 = 4,7 mm
Tpmax = [(2·)/265] · 0,165 = 0,15 ms
Vpmax = 265 ·0,331 = 87,7 m/s
Po = 470 · 0, 237 = 111 bar
To = [(2·123)/265]·0,754= 70 ms
Il valore di
sarà dato da 123/ 4,7 = 26,17
Le formule non tengono conto della perdita di pressione tra tamburo e canna nei revolver.
Velocità dei gas alla bocca
I gas di sparo escono dalla bocca con grande velocità che, per le pistole, supera quella del proiettile; essi quindi, per un breve tratto, oltrepassano il proiettile.
La velocità dei gas può essere calcolata con la formula di Laval
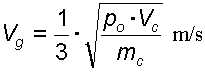 in cui Vc ed mc sono i valori già visti sopra.
La velocità del proiettile a seconda della lunghezza della canna - Calcolo semplificato.
La velocità del proiettile, oltre che dal tipo di cartuccia, dipende da vari fattori quali la maggiore o minore marcata forzatura fra le righe della canna, la perdita di energia meccanica conseguente all'attrito all'interno dell'anima, dalle condizioni atmosferiche che influenzano la combustione della carica di lancio, per tacere poi dello stato di conservazione della cartuccia.
In genere i fabbricanti indicano la velocità del proiettile delle loro cartucce; i dati sono in genere riferiti a canne di prova di 60 cm di lunghezza, con caratteristiche ottimali, e sono valori medi che possono divergere anche del 5% rispetto alla velocità effettiva. Quando non sia possibile misurare direttamente la velocità del proiettile, ci si dovrà affidare a calcoli teorici.
Il fattore principale di cui occorre tener conto è quello della lunghezza delle canna in quanto, specie nelle armi corte, la velocità reale del proiettile può essere di gran lunga inferiore a quella che ci si potrebbe attendere leggendo i dati delle case produttrici. Nei revolver inoltre è necessario tener conto della perdita di pressione dovuta alla maggior o minor fuga di gas fra tamburo e canna (in termini di energia, la perdita può variare dal 10 al 20%).
La variazione di velocità dipendente dal variare della lunghezza della canna, naturalmente entro limiti ragionevoli (per una pistola non avrebbe senso una canna lunga meno di 4 cm o più di 40 cm), può essere calcolata in modo alquanto approssimativo assumendo che la variazione di velocità sia proporzionale alla radice quarta degli spazi percorsi dai proiettili nelle rispettive canne. Lo spazio percorso si calcola misurando la lunghezza che intercorre tra la punta del proiettile e la bocca della canna, aggiungendo poi ad essa la lunghezza del proiettile. Si avrà quindi
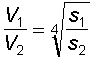 Se, ad esempio un proiettile di pistola sviluppa 320 m/s in una canna di 15 cm., in una canna di 5 cm la velocità sarà di
Risultati molto più precisi possono ottenersi se si tiene conto anche della progressività della polvere individuata in base ad una costante. Questa può essere ricavata dalla velocità iniziale del proiettile se si conosce il peso della polvere e la lunghezza della canna.
Sia:
S = percorso del proiettile in mm nella canna, misurato dalla base del proiettile nella cartuccia alla bocca dell'arma.
C = calibro in mm
P = peso del proiettile in gr
M = peso della polvere il gr
R = costante di progressività della polvere
La balistica interna ci insegna che la velocità del proiettile sarà data dalla formula (Weigel)
da cui si ricava che
Stabilita per una determinata cartuccia e una certa lunghezza di canna, la velocità iniziale del proiettile e quindi il valore di R, sarà facile calcolare la velocità per una diversa lunghezza di canna o per una diversa carica, introducendo il valore di R nella penultima formula. Ho predisposto un piccolo programma da scaricare e che esegue questo calcolo.
Si prenda ad esempio un proiettile cal 9 Para con palla di gr. 7,5 e carica di polvere di 0,26 gr, che sviluppa una velocità iniziale di 332 m/s e supponiamo che sia stato sparato in una canna di 120 mm con un percorso del proiettile pari a 105 mm e senza perdite di gas. La costante R sarà pari a 1716. Se ora assumiamo di impiegare una canna di 80 mm, con un percorso libero del proiettile pari a 65 mm, ed inseriamo questi due valori nella formula di Weigel, otterremo che la velocità iniziale si sarà ridotta a 294 m/s.
TABELLA I dei fattori di Heydenreich
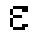A B C D F
0.25 0.0313 0.139 0.324 0.216 0.725
0.26 0.0330 0.146 0.326 0.220 0.732
0.27 0.0347 0.152 0.327 0.226 0.740
0.28 0.0365 0.159 0.329 0.231 0.747
0.29 0.0383 0.165 0.331 0.237 0.755
0.30 0.0402 0.172 0.333 0.242 0.762
0.31 0.0421 0.178 0.335 0.250 0.770
0.32 0.0440 0.186 0.337 0.256 0.777
0.33 0.0460 0.193 0.339 0.263 0.785
0.34 0.0480 0.200 0.341 0.269 0.792
0.35 0.0500 0.207 0.343 0.278 0.800
0.36 0.0521 0.214 0.345 0.282 0.807
0.37 0.0542 0.222 0.347 0.288 0.814
0.38 0.0563 0.229 0.350 0.294 0.822
0.39 0.0585 0.237 0.351 0.300 0.829
0.40 0.0608 0.244 0.354 0.304 0.836
0.41 0.0631 0.252 0.356 0.313 0.844
0.42 0.0654 0.260 0.359 0.319 0.851
0.43 0.0678 0.268 0.361 0.325 0.858
0.44 0.0703 0.276 0.364 0.332 0.866
0.45 0.0729 0.284 0.366 0.340 0.873
0.46 0.0756 0.292 0.369 0.346 0.880
0.47 0.0784 0.301 0.371 0.354 0.888
0.48 0.0813 0.309 0.374 0.363 0.895
0.49 0.0843 0.318 0.377 0.372 0.902
0.50 0.0875 0.326 0.380 0.382 0.910
0.51 0.0908 0.335 0.383 0.394 0.918
0.52 0.0944 0.343 0.386 0.407 0.926
0.53 0.0981 0.352 0.390 0.421 0.934
0.54 0.1020 0.361 0.393 0.437 0.942
0.55 0.1061 0.370 0.396 0.454 0.950
0.56 0.1099 0.379 0.399 0.470 0.958
0.57 0.1141 0.388 0.403 0.487 0.966
0.58 0.1185 0.397 0.406 0.505 0.974
0.59 0.1230 0.406 0.409 0.524 0.983
TABELLA 2 dei fattori di Heidenreich
 G H J
0.25 0.741 0.392 0.610
0.50 0.912 0.635 0.780
0.75 0.980 0.834 0.903
1.00 1.000 1.000 1.000
1.25 0.989 1.130 1.081
1.50 0.965 1.262 1.154
1.75 0.932 1.366 1.219
2.00 0.898 1.468 1.282
2.50 0.823 1.632 1.394
3.00 0.747 1.763 1.495
3.50 0.675 1.875 1.589
4.00 0.604 1.983 1.682
4.50 0.546 2.068 1.769
5.00 0.495 2.140 1.851
6.00 0.403 2.269 2.012
7.00 0.338 2.363 2.163
8.00 0.284 2.445 2.309
9.00 0.248 2.509 2.451
10.00 0.220 2.566 2.589
11.00 0.199 2.615 2.725
12.00 0.181 2.659 2.858
13.00 0.164 2.702 2.988
14.00 0.150 2.740 3.116
15.00 0.137 2.777 3.253
16.00 0.125 2.811 3.390
17.00 0.117 2.837 3.502
18.00 0.109 2.862 3.618
19.00 0.102 2.887 3.740
20.00 0.096 2.910 3.816
25.00 0.073 3 003 4 455
30.00 0.058 3.075 5.031
35.00 0.048 3.162 5.657
40.00 0.041 3.223 6.261
BALISTICA TERMINALE
La balistica terminale studia il comportamento del proiettile nel bersaglio. Qui ci occuperemo solo di quei pochi problemi di balistica terminale che possono essere oggetto di una valutazione matematica, riservando ad un'altra voce la trattazione dei fenomeni attinenti piuttosto alla medicina legale.
Uno dei fenomeni che meglio si presta ad uno studio scientifico è quello della penetrazione del proiettile nei vari mezzi, pur considerando che la diversità dei materiali e la diversità di comportamento dei singoli proiettili, a seconda della loro struttura e della velocità al momento dell'impatto, non consentono il ricorso ad un modello matematico generale, ma soltanto a formule empiriche. Accade infatti, da un lato, che proiettili ad alta velocità si deformino facilmente all'impatto e, d'altro lato, che proiettili molto veloci non facciano a tempo a trasferire la loro energia al bersaglio.
Punto di partenza per calcolare la penetrazione del proiettile nella maggior parte dei materiali è la sua energia cinetica o forza viva; essa può essere calcolata con la formula
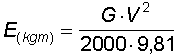 in cui G rappresenta il peso in grammi e V la velocità in m/s. Se si elimina il valore 9,81 si ottiene il risultato in Joule (1kgm = 9,81 J). Qui trovate un piccolo programma per il suo calcolo in Joule..
Le formule che proporremo sono state elaborate per proiettili di pistola incamiciati ed a punta tondeggiante e presuppongono un impatto sul bersaglio ad angolo retto. Se il proiettile colpisce il bersaglio con un angolo minore, il che può accadere per effetto dei movimenti di precessione, anche se il piano del bersaglio è perpendicolare alla traiettoria), la sua capacità di penetrazione sarà naturalmente minore fino a giungere, oltre un certo angolo, al rimbalzo.
Nell'attraversare materiali in più strati può anche accadere che il proiettile, che inizia a penetrare già inclinato, venga ulteriormente deviato nell'attraversamento del primo strato, così da non essere più in grado di attraversare il secondo su cui scivola semplicemente (è all'incirca il fenomeno per cui un raggio di luce viene rifratto quando dall'aria penetra nell'acqua). In linea di massima i risultati ottenibili con le formule sono utilizzabili anche per proiettili di carabina e per proiettili non incamiciati in quanto lo scarto nella penetrazione rispetto al proiettile tipo, se non intervengono deformazioni, può assumersi come costante e lineare e quindi facilmente verificabile in via sperimentale; ad esempio si riscontra sperimentalmente che la penetrazione di proiettili di piombo nel legno o nel ferro è inferiore di circa il 20% rispetto a quella di un proiettile incamiciato di eguale calibro. Particolare cautela occorre nell'applicare le formule a proiettili semicamiciati, proprio per la grande varietà di deformazioni che possono subire. Nelle formule che seguito i simboli sono usati, salvo diversa indicazione, con il seguente significato:
P: penetrazione in cm riferita alla punta del proiettile
E: in chilogrammetri
V: velocità di impatto in m/s
G: peso in grammi
C: calibro in mm.
S: sezione del proiettile in cmq
Penetrazione nel ferro
La penetrazione di proiettili nel ferro (blindature, carrozzerie, ecc.) è stata oggetto di ampi studi in campo militare e la formula più usata è quella di Krupp
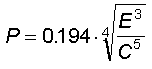 con cui possono risolversi problemi quali:
- un proiettile di pistola cal. 9 Para può perfora la blindatura di un'auto a 100 metri di distanza?
- quale velocità possiede il proiettile dopo aver perforato una lamiera di un millimetro?
Si badi che la formula di Krupp è valida solo per l'attraversamento di uno strato omogeneo di metallo; ad esempio un proiettile cal 9 Para perfora alla velocità di 330 m/s una piastra di circa 2,1 mm di spessore o tre piastre da 0.7 mm pressate assieme; se invece le tre piastre sono distanziate l'una dall'altra, ad es. di un centimetro si assiste al fenomeno un po' paradossale ma scientificamente spiegabile, per cui ne perfora ben 15 per un totale di 10,5 mm ! Si veda apposita voce La perforazione di lastre sottili
Penetrazione nel legno
La penetrazione nel legno di abete è presa comunemente come indice dell'efficacia di un proiettile. Essa può essere calcolata con la formula di Weigel
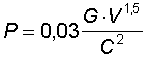
oppure con quella di Hatscher che ha il vantaggio di tener conto del fattore di forma i, il che è utile specialmente per proiettili di fucile
Penetrazione nell'osso
La formula che per proiettili idi pistola incamiciati fornisce i migliori risultati è
Per proiettili a punta arrotondata si deve sostituire la costante 0,44 con 0,30 e per proiettili wad-cutter con la costante 0,15.
Dalla velocità al momento dell'impatto vengono detratti 60 m/s che rappresentano la perdita di velocità per effetto del solo impatto; ciò significa, in altre parole, che un proiettile con velocità inferiore a 60 m/s produce sull'osso solo un effetto contusivo, ma non ne spezza il tessuto. Questa cosiddetta velocità limite di 60 m/s è riferita a proiettili per pistola a punta tondeggiante o a palle sferiche; nel caso di proiettili con elevata densità sezionale oppure molto appuntiti, è chiaro che la velocità limite sarà inferiore. Se il proiettile attraversa altri tessuti (indumenti, muscolo), bisognerà ovviamente tenerne conto.
Il Sellier fornisce anche la formula per calcolare la perdita di velocità al passaggio di un certo spessore di osso. La formula è
Vr = Velocità residua
Vo = Velocità operante dopo aver tolto i 60 ms liminari
Calibro in cm
Peso in grammi
S spessore osso perforato in cm
Vr = Vo* [(1 - 2,3 * (10^4/Vo^2) * S*C/G)]^(1/2)
Ad esempio se un proiettile C = 0,635 di P = 3,2 gr inizia a lavorare sull'osso a 120 m/s , nel perforare 0,5 cm perderà 10 m/s (esempio del Sellier).
Penetrazione nella cute
Il limite di velocità a cui un proiettile è ancora in grado di bucare la cute umana è stata studiata per proiettili di pistola o per palle sferiche e risulta valida la formula del Sellier
in cui Ds rappresenta la densità sezionale. Questa è data dal rapporto G/S.
Dalla formula si ricava, ad esempio, che un pallino da caccia di 3 mm di diametro non riesce a perforare la pelle, ma procura solo una contusione, se non raggiunge la velocità di 78 m/s.
La stessa formula può essere usata anche per indumenti; sostituendo il valore +100 a +22 si ha la velocità limite per la tuta da combattimento americana a sei strati di tessuto.
Il Kneubuehl ha successivamente ridefinito il concetto di velocità limite, come quella del proiettile (o scheggia) che con grande probabilità su di un corpo nudo non provocherà alcun danno, individuando quindi l’energia limite in 0,1 J/ mm2 per la cute e in 0,06 J /mm2 per l’occhio. L’esperienza insegna che un giocattolo soft-air può provocare danni all’occhio di un bambino già con 0,025 J /mm2.
Si ottiene quindi la seguente tabella.
|
Proiettile
|
Peso
|
Cute
|
Occhio
|
|
|
gr
|
Vl / ms
|
E / J
|
Vl / ms
|
E / J
|
|
2 mm pallino
|
0.047
|
116
|
0,3
|
90
|
0,2
|
|
3 mm pallino
|
0,16
|
94
|
0,7
|
73
|
0,4
|
|
4 mm pallino
|
0,38
|
81
|
1,3
|
63
|
0,8
|
|
4,5 diabolo
|
0,53
|
77
|
1,6
|
60
|
1,0
|
|
22 l. r.
|
2,55
|
44
|
2,5
|
34
|
1,5
|
|
9 mm para
|
8
|
40
|
6,4
|
31
|
3,8
|
|
38 special
|
10,2
|
35
|
6,4
|
27
|
3,8
|
|
45 Auto
|
14,8
|
37
|
10,2
|
29
|
6,1
|
|
223 Rem.
|
3,56
|
37
|
2,4
|
29
|
1,5
|
|
7,62x39 Kal.
|
8
|
34
|
4,6
|
26
|
2,7
|
|
7,5 GP11
|
11,3
|
28
|
4,4
|
22
|
2,7
|
Si tenga presente che un proiettile pesante con Energia superiore a 4 J provoca comunque un ematona.
Per ottenere valori di sicurezza non si dovrebbe superare la metà del valore di E indicato in tabella.
Penetrazione nei tessuti molli del corpo umano
Sulla base di studi compiuti sulla gelatina balistica il Sellier è pervenuto alla formula
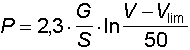 in cui dalla velocità di impatto V viene detratta la velocità limite relativa alla cute, il cui spessore viene però computato come spessore di tessuto muscolare
Le formule sopra riportate non sono solamente delle curiosità matematiche, ma possono orientare nella soluzione di problemi di balistica giudiziaria, di cui si riportano alcuni esempi.
1) Un uomo è stato colpito da un colpo di pistola da circa 100 metri di distanza che ha forato il cranio da parte a parte per complessivi cm. 1 di osso; è possibile che sia stata usata una cal. 7,65 ACP?
Un tale proiettile con velocità iniziale di 285 m/s, a 100 metri ha ancora una velocità di 240 m/s. Le perdite di velocità che subisce all'impatto sono di 35 m/s per impatto con la cute e di 60 m/s per l'impatto sull'osso; 10 m/s li perde nella perforazione dei primi 5 mm. di osso ed entra quindi nel cervello alla velocità di 135 m/s; a questa velocità perfora 12 cm di tessuti molli perdendo altri 35 m/s; ulteriori 60 m/s li perde all'impatto con la parete opposta del cranio e altri 10 m/s per la sua perforazione. Residuano quindi solo 30 m/s, proprio al limite della possibilità della completa perforazione (sperimentalmente si è accertato che da distanza ravvicinata solo l'80% dei proiettili cal 7,65 perfora il cranio da parte a parte; è quindi possibile, ma improbabile che vi sia riuscito a 100 metri di distanza).
2) Una persona viene colpita da un colpo cal. 9 Para da circa 100 metri di distanza, con perforazione della colonna vertebrale e fuoriuscita dalla parte opposta. È sufficiente un colpo di pistola (V= 280 m/s) o deve ipotizzarsi un colpo di mitra (V= 400 m/s) ?
Le perdite di velocità sono di 60 m/s per impatto e attraversamento cute ed abiti, 60 m/s per impatto con l'osso spesso 2 cm, 20 m/s per la sua perforazione; rimangono solo 140 m/s insufficienti per perforare tutto il ventre e la cute e gli abiti nella parte anteriore; deve quindi ipotizzarsi che il colpo sia stato sparato con un mitra.
Attenzione; nel fare questi calcoli attenzione a non sottrarre due volte la velocità limite!
Penetrazione in materiali vari
Per il calcolo della penetrazione in vari materiali, quali terra o mattoni, si può usare la formula di Petry in cui P è il peso in gr, C il calibro in mm, V la velocità di impatto in ms e k un coefficiente con il seguente valore
|
0,016
|
Acciaio
|
|
0,025
|
lega di acciaio
|
|
0,64
|
muro di cemento
|
|
0,94
|
muro di pietra
|
|
1,63
|
muro di mattoni
|
|
2,29
|
terreno sabbioso
|
|
3
|
terreno normale erboso
|
|
0,336
|
pietra calcarea
|
|
4,565
|
terreno soffice
|
|
5,87
|
terreno argilloso
|
La formula richiede che lo spessore totale del materiale sia almeno tre volte quello calcolato; se è inferiore, la penetrazione aumenta.
La penetrazione Pn ( o D) in cm sarà data da
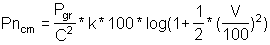
oppure, se proprio si vuole la formula nella sua originaria precisione matematica
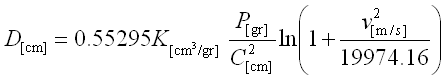
Quale riscontro si tenga presente che per un proiettile di pistola cal 7,65, la penetrazione in terra sabbiosa sarà di circa 17 cm. Qui trovate un piccolo programmino per eseguire il calcolo.
Penetrazione sperimentale in cm del proiettile militare 30-06 (Vo =845 m/s, P= 9,7 g) alla distanza di 180 metri
media massima
Ghiaia 17,7 20
Muro di mattoni 11 16.5
Sabbia asciutta 18,5 20,7
Sabbia bagnata 18,5 23,3
Argilla 62 73,5
Terra sciolta 50 50
- estratto dal sito : www.earmi.it
|
|
|
|
|
|
| |
L'Aserc ha avuto fino ad oggi 226600 visitatori (868545 hits) GRAZIE!!! |
|
|
|
|
|
|
|
